Метод Фибоначчи - использование чисел ряда в поисках решений

Многие математики прославились тем, что открыли закономерности, которые впоследствии позволили решать широкий круг самых разнообразных задач. Причем относятся они не только к чисто математической, но и к иным областям деятельности человека. Рассмотрим в качестве примера метод Фибоначчи, базирующийся на за так называемом «золотом числе».

Его значение приблизительно равняется 1,618 (в некоторых случаях используется обратное значение 0,618). Оно вычисляется как соотношение между двумя соседними Фибо-числами. При увеличении их порядковых номеров это соотношение стремится к:

1,618 – если Фибо-число с порядковым номером (K+1) делится на Фибо-число с порядковым номером К;
0,618 – если Фибо-число с порядковым номером K делится на Фибо-число с порядковым номером (К+1).

Рассматриваемый нами метод чисел Фибоначчи используется для нахождения экстремумов какой-либо целевой функции. Данная задача может использоваться почти во всех сферах, где необходимо отыскать оптимальный параметр, при котором основанная на нем функциональная зависимость будет давать максимум или минимум. Если взять для примера финансовую сферу, то подобная задача может заключаться в поиске такого распределения инвестиционного капитала между инвестиционными продуктами с разными условиями, при котором получаемая прибыль будет максимальной.

Суть метода поиска Фибоначчи

Для его реализации необходимо явное задание целевой функции. Оно характеризуется тем, что в его левой части находится только оптимизируемый параметр, а в правой – все остальные параметры, значения которых можно варьировать в заданных пределах. Для простоты будем считать, что такой варьируемый параметр будет всего один.

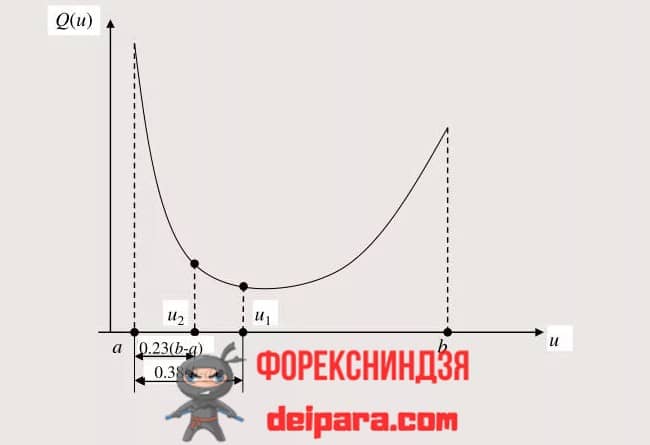
Рисунок 1. График, поясняющий поиск методом чисел Фибоначчи.

Тогда функциональную зависимость можно представить в виде одномерной кривой, построенной на прямоугольной координатной плоскости (рис. 1). В этом случае метод Фибоначчи будет заключаться в задании границ отрезка, на котором должен находиться экстремум. Допустим это интервал (a;b). Тогда он делится на три части так, что два длина двух отрезков, прилегающих к концам этого интервала, будет одинаковой и принимается за 1-у условную единицу, а длина отрезка находящегося в середине этого интервала будет равна 0,618 условных единиц. Затем в точках, которыми интервал поделен на 3 части, находится значение функции и за новый конец нового интервала принимается та точка, в которой вычисленное значение функции больше (если ищется минимум) или меньше (если ищется максимум). Далее этот новый интервал снова делится на 3 части и шаги повторяются.

Для такого метода поиска Фибоначчи дополнительно количество делений, поскольку оценить точность на каждой итерации невозможно.

Использование в трейдинге метода Фибоначчи (пример)

При анализе динамики рынков метод чисел Фибоначчи применяется несколько иным способом – предполагается, что через интервалы, кратные отношениям между этими числами, возникают вполне определенные рыночные состояния. Причем эти интервалы могут отсчитываться по шкале котировок, по временной шкале или по ним обоим сразу. В качестве примера рассмотрим самый популярный и простейший инструмент анализа по методу Фибоначчи, называющийся «Линии».

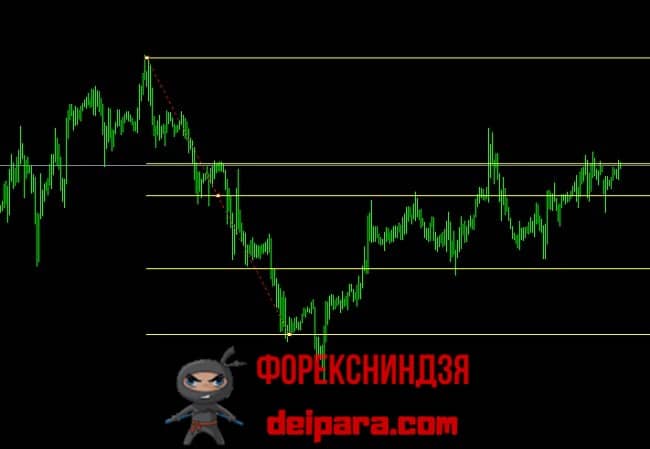
Рисунок 2. Линии Фибоначчи – метод поиска начала коррекций.

С его помощью график котировки размещается горизонталями, положение которых отмечает уровни, на которых вероятнее всего возникнут трендовые откаты (рис. 2). При этом за контрольное расстояние, по которому и происходит расчет уровневой разметки, принимается амплитуда (т. е. расстояние от экстремума до экстремума) предшествующего тренда. Этот пример метода Фибоначчи обеспечивает разметку по шкале котировки.

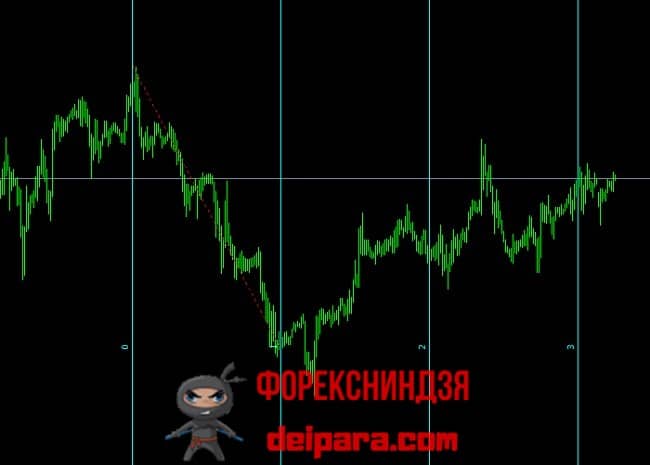
Рисунок 3. Метод чисел Фибоначчи, реализованный в индикаторе «Временные зоны».

А в качестве примера разметки по шкале времени рассмотрим временные зоны Фибоначчи (рис. 3). Они также строятся по экстремумам завершившегося последнего тренда, но разметка состоит из вертикалей. Их положение указывает на вероятное время формирования локальных экстремумов следующего тренда.